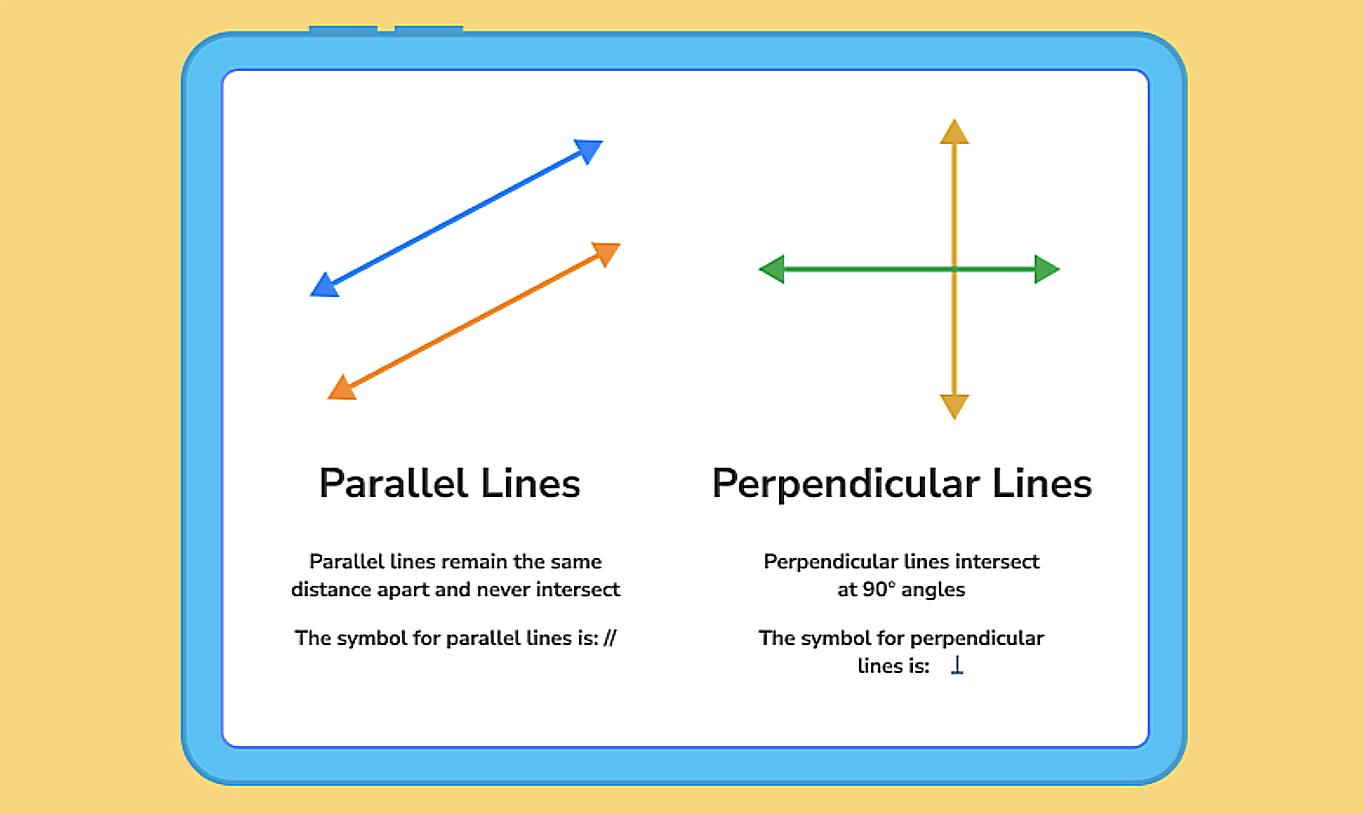
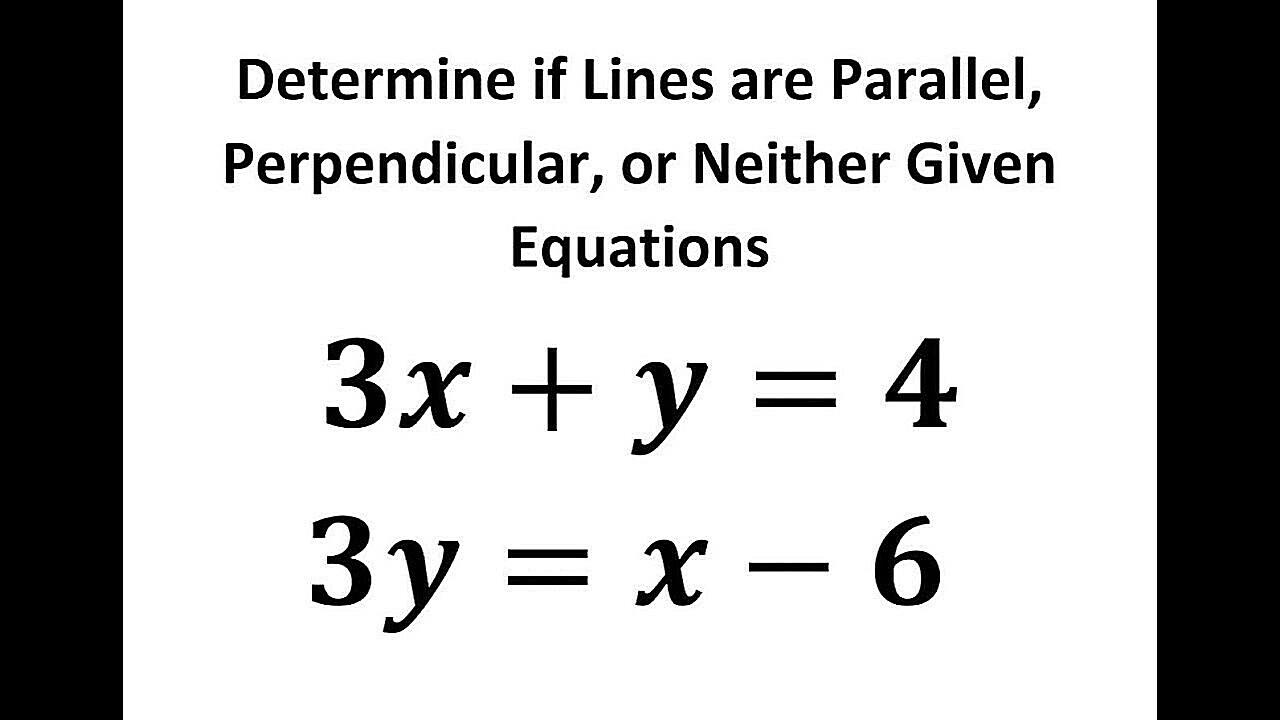How To Prove That Diagonals Are Perpendicular : Berrysbooks

How To Prove That Diagonals Are Perpendicular

Beautiful Work Tips About Is Wireframe A Paper Prototype

Painstaking Lessons Of Tips About Is 6% Voltage Drop Ok

Spotting Right Angles

1. Understanding Perpendicularity

Have you ever stared at a crossroads and thought, “Wow, those lines are really… perpendicular?” Probably not. But understanding perpendicularity is actually quite useful, from hanging pictures straight to understanding the angles in your latest DIY project. In simple terms, “How to tell if a line is perpendicular” boils down to recognizing those perfect 90-degree angles. It’s all about right angles, baby! Think of the corner of a square or rectangle — that’s what we’re aiming for.

So, what exactly is a perpendicular line? Well, it’s a line that meets another line at a right angle. A right angle, as you might remember from geometry class (or perhaps a hazy memory of it), is an angle that measures exactly 90 degrees. Imagine a perfectly upright flagpole casting a shadow on flat ground — the flagpole and its shadow form a pretty good representation of perpendicular lines. The keyword term here is “perpendicular” which in this context, is an adjective describing the relationship between the two lines.

Why should you even care? Because perpendicularity pops up everywhere! Architecture, engineering, design, even video games rely on right angles for stability, clarity, and just plain looking good. Imagine building a house with walls that weren’t perfectly perpendicular to the floor. You’d have slanted paintings, rolling marbles, and a general sense of unease. Nobody wants that!

This article will equip you with the knowledge and tools to confidently identify perpendicular lines in the wild. We’ll cover the key concepts, show you practical techniques, and even throw in a few helpful tips and tricks. Get ready to become a right-angle-detecting ninja!

Methods for Determining Perpendicularity

2. Visual Inspection and Estimation

The simplest way to check for perpendicularity is to just eyeball it. Seriously! If you’re dealing with something like hanging a picture, a quick visual assessment can often be enough. Compare the angle you see to a known right angle, like the corner of a piece of paper or a credit card. If it looks close, it probably is! Just don’t rely on this method for anything critical, like building a bridge (please don’t build bridges after only reading this).

Think of it like estimating the height of a building. You might not get it exactly right, but you can usually get a pretty good idea. The same goes for perpendicular lines. Practice makes perfect, so the more you look for right angles in your environment, the better you’ll become at spotting them. Plus, you’ll impress your friends with your newfound right-angle-detecting abilities! “Wow, Brenda, that fence post is remarkably perpendicular!”

Remember that even a slight deviation from 90 degrees can have a significant impact over distance. Imagine a building where the walls are only off by a degree or two. By the time you get to the roof, the walls could be noticeably slanted. So, while visual inspection is a good starting point, it’s not always the most accurate.

When visually inspecting, look for any obvious leaning or tilting. Does one line appear to be slanting towards or away from the other? If so, they’re probably not perpendicular. Try using a straight edge, like a ruler or a piece of cardboard, to help you visualize the angles more clearly. The more you practice, the better you’ll get at spotting those pesky non-perpendicular lines!

3. Using a Protractor

For a more precise measurement, break out the protractor! This trusty tool is designed specifically for measuring angles, making it perfect for determining if two lines are truly perpendicular. Place the center point of the protractor at the intersection of the two lines, and align one of the lines with the 0-degree mark. Now, read the angle measurement where the other line intersects the protractor scale. If it reads 90 degrees, congratulations! You’ve got yourself a pair of perpendicular lines.

Protractors come in different shapes and sizes, but they all work on the same basic principle. Some are semi-circular, while others are full circles. Some have digital displays, while others use a traditional analog scale. Choose the type that you find most comfortable and easy to use. Just make sure it’s accurate! A faulty protractor will lead to faulty measurements, and nobody wants that.

When using a protractor, make sure it’s properly aligned with the lines you’re measuring. A slight misalignment can throw off your measurement, so take your time and double-check your work. If you’re having trouble seeing the scale clearly, try using a magnifying glass. And remember, practice makes perfect! The more you use a protractor, the more comfortable and confident you’ll become.

Beyond simple angle measurement, protractors can also be used to create perpendicular lines. If you need to draw a line that’s perpendicular to an existing line, simply use the protractor to mark a 90-degree angle at the desired point. Then, use a ruler or straight edge to draw the line through that mark. Voila! A perfectly perpendicular line, ready for action.

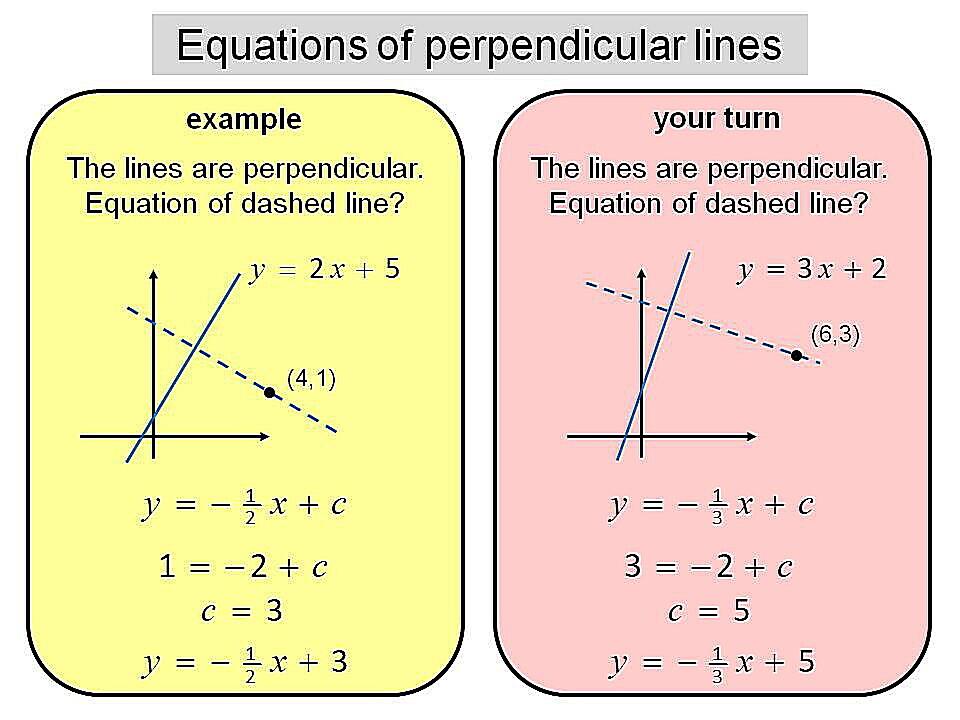
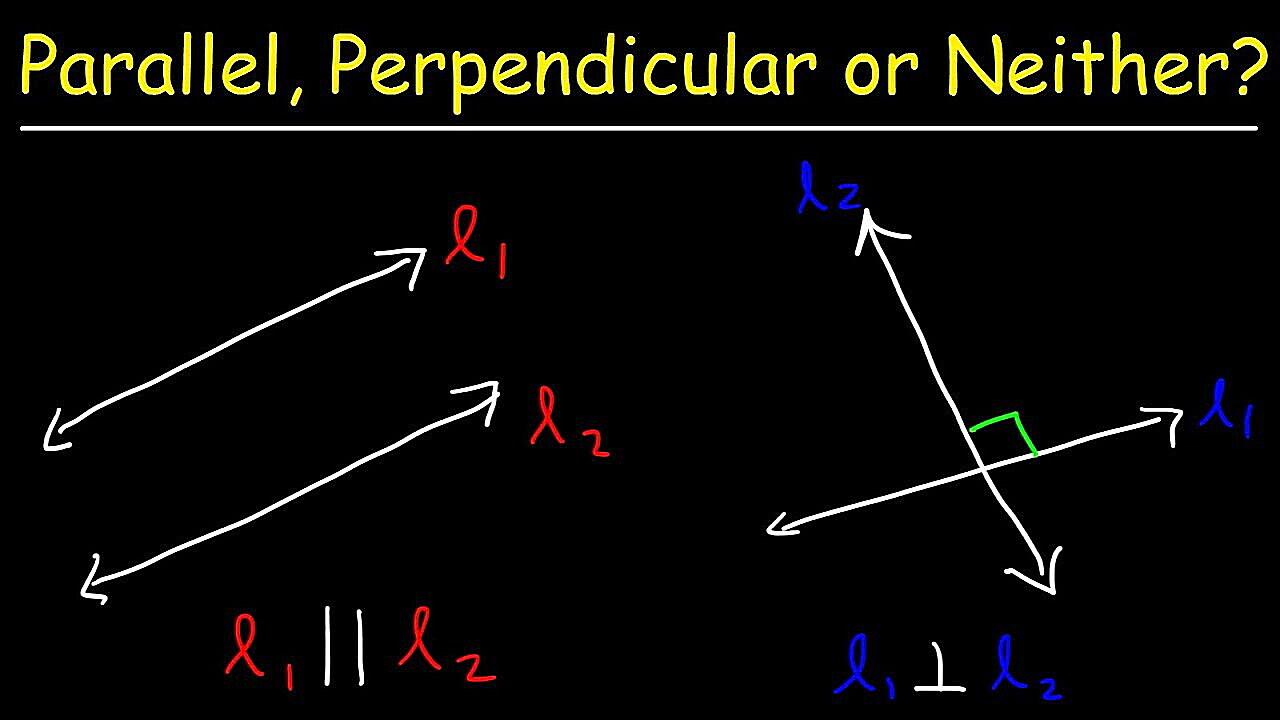
4. The Slope Method

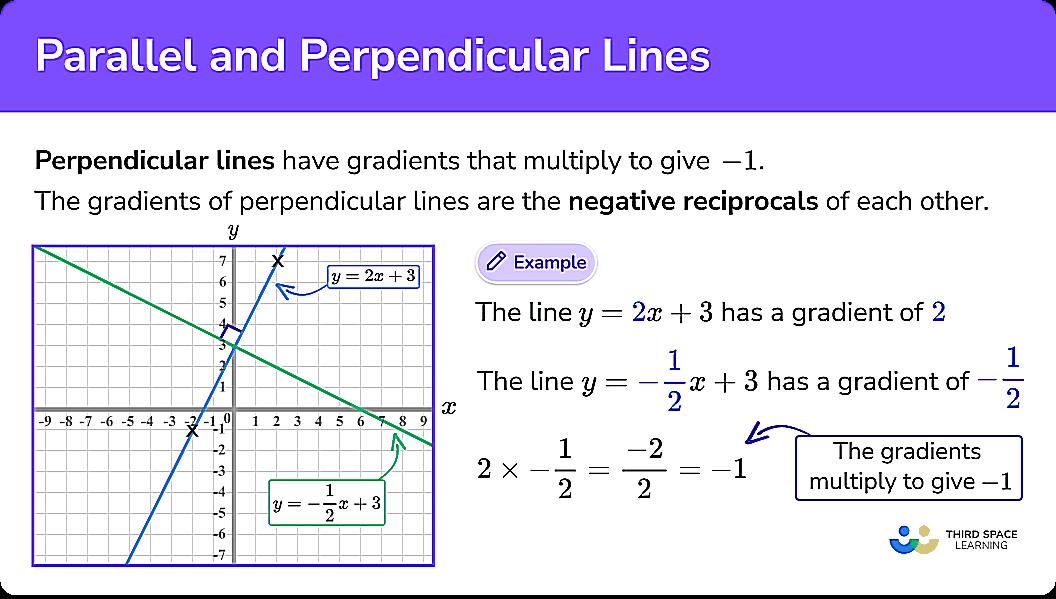
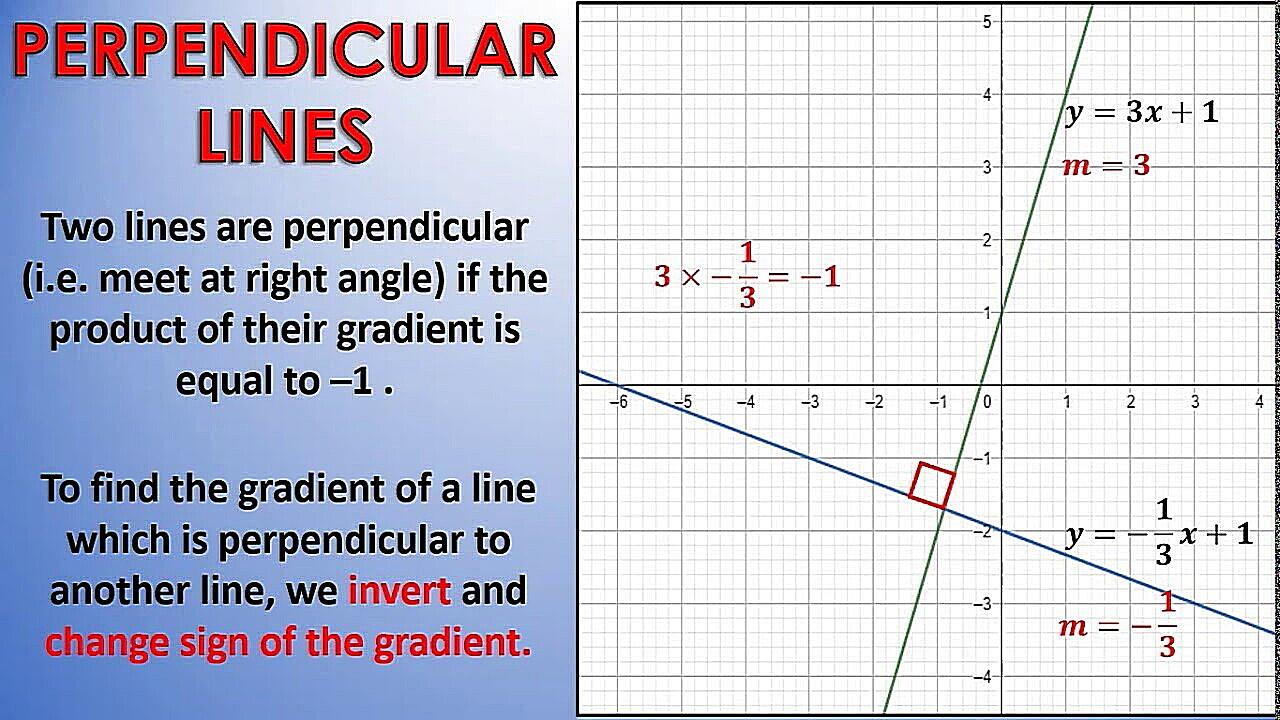
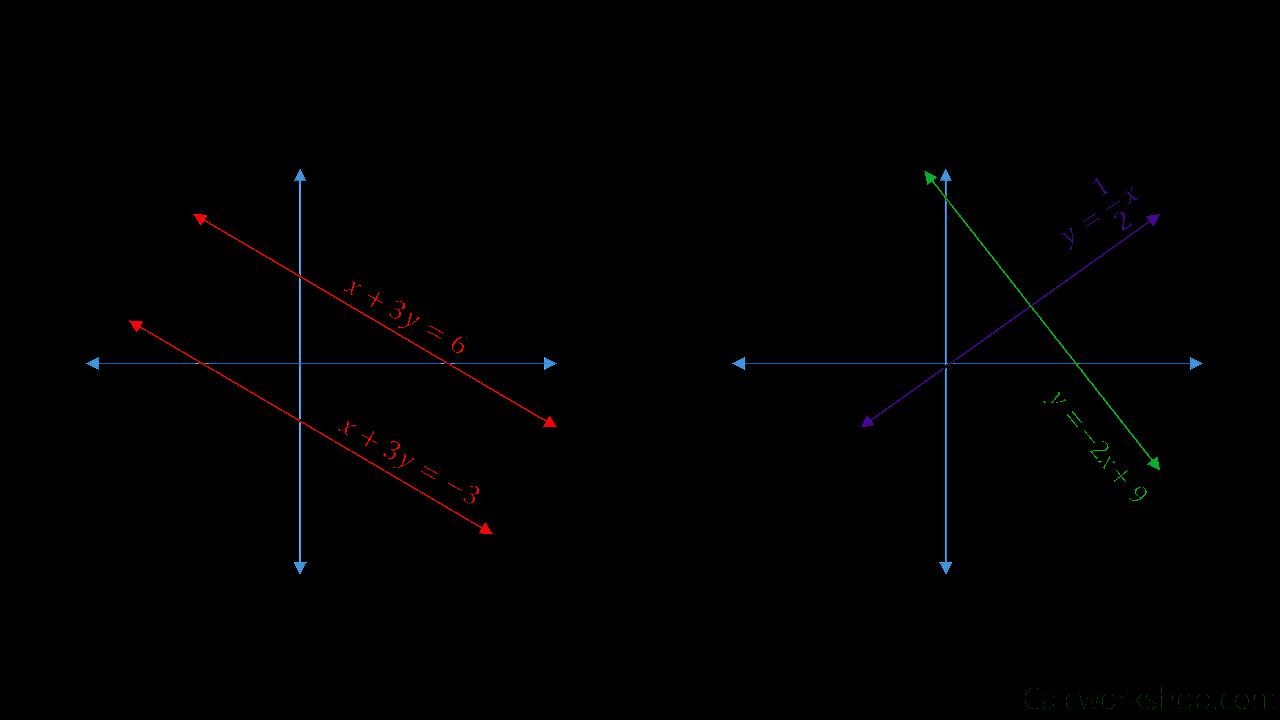
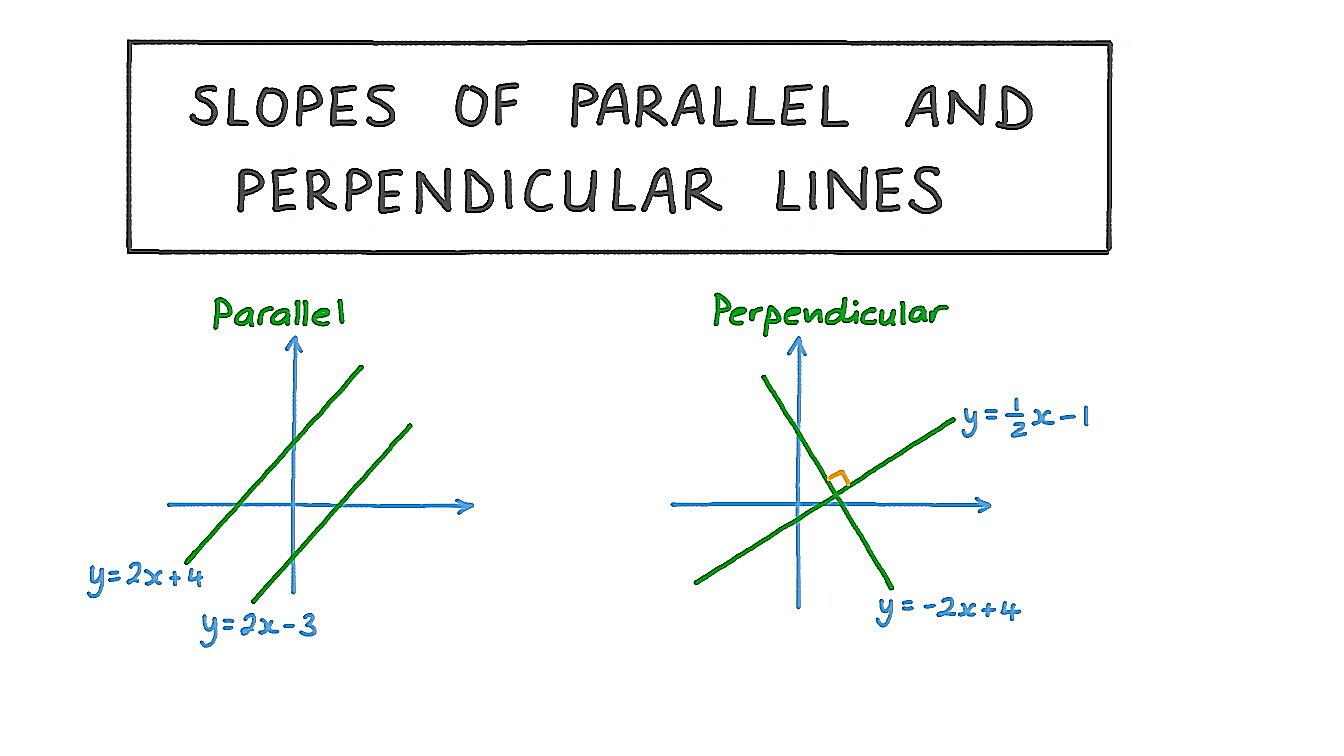
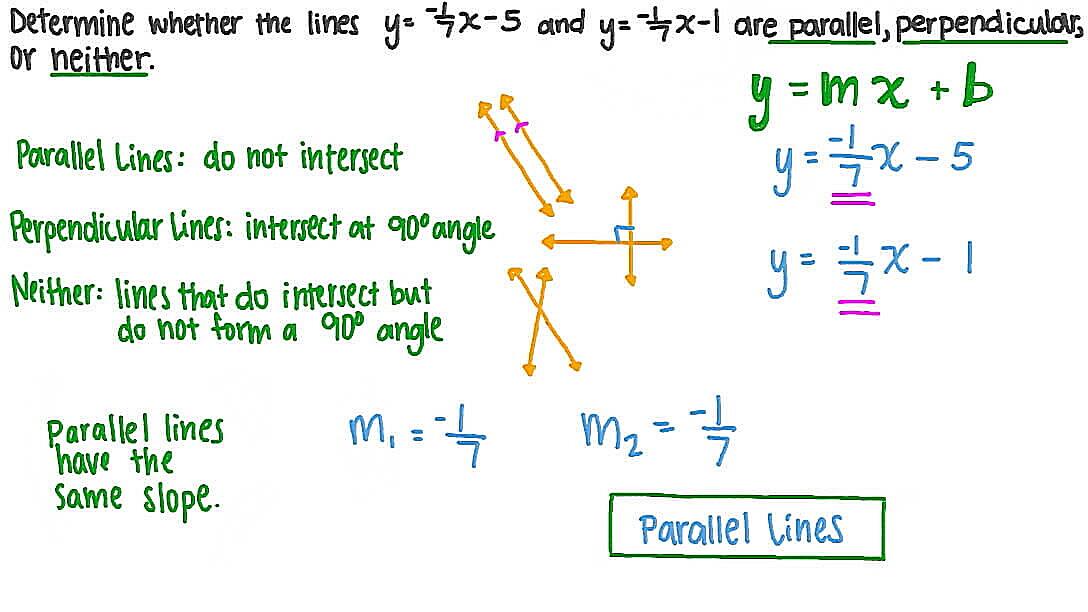
If you’re working with lines on a coordinate plane, you can use the slope method to determine perpendicularity. The slope of a line is a measure of its steepness and direction. Two lines are perpendicular if and only if the product of their slopes is -1. In other words, if one line has a slope of ‘m’, the slope of a line perpendicular to it will be ‘-1/m’. Sounds complicated? Don’t worry, we’ll break it down.

First, you need to find the slopes of the two lines. Remember the formula: slope (m) = (y2 – y1) / (x2 – x1), where (x1, y1) and (x2, y2) are any two points on the line. Calculate the slopes of both lines using this formula. Then, multiply the two slopes together. If the result is -1, then the lines are perpendicular. If it’s anything else, they’re not.

Let’s say you have one line with a slope of 2. A line perpendicular to it would have a slope of -1/2 (which is -0.5). Multiply them together: 2 * (-0.5) = -1. Bingo! Perpendicular lines! This method is particularly useful when you’re working with equations of lines, as you can easily determine their slopes from the equations.

This method works because the slope represents the “rise over run” of a line. A line with a positive slope rises as you move to the right, while a line with a negative slope falls. Perpendicular lines have slopes that are negative reciprocals of each other, which means that one line rises while the other falls, and their rates of change are inversely related. This ensures that they intersect at a perfect 90-degree angle.

Tools to Help You Check Perpendicularity

5. Speed Squares and Combination Squares

For woodworking and construction projects, a speed square or combination square is your best friend. These handy tools are designed to quickly and accurately mark right angles. A speed square is a triangular tool with a 90-degree angle, while a combination square has an adjustable head that can be set to any angle, including 90 degrees. Simply align the square with one of the lines you want to check, and see if the other line aligns with the square’s edge. If it does, you’ve got perpendicularity!

These squares are incredibly versatile and can be used for a variety of tasks, from marking cut lines to checking the squareness of corners. They’re a must-have for any DIY enthusiast or professional tradesperson. Plus, they’re relatively inexpensive and easy to find at any hardware store. Just make sure to choose a square that’s made of durable material, like steel or aluminum, so it can withstand the rigors of everyday use.

Beyond checking for perpendicularity, these squares can also be used to draw perpendicular lines. Simply align the square with an existing line and use its edge as a guide to draw a new line at a 90-degree angle. This is particularly useful when you need to create a precise right angle for a woodworking joint or other construction project.

When using a speed square or combination square, make sure it’s clean and free of debris. A dirty or damaged square can lead to inaccurate measurements, so take good care of your tools. Store them in a safe place when you’re not using them, and clean them regularly with a soft cloth.

6. Laser Levels

For larger projects or situations where precision is paramount, consider using a laser level. These devices project a laser beam that creates a perfectly level or plumb line, which you can then use as a reference to check for perpendicularity. Some laser levels even have built-in angle measuring capabilities, making it even easier to determine if two lines are at a right angle to each other.

Laser levels are particularly useful for tasks like installing tile, hanging cabinets, or building walls. They can save you a lot of time and effort compared to traditional methods, and they can also help you achieve a higher level of accuracy. However, they can be a bit more expensive than other tools, so consider your budget and the frequency with which you’ll be using them before making a purchase.

When using a laser level, be sure to follow the manufacturer’s instructions carefully. Laser beams can be harmful to your eyes, so never look directly into the beam. Also, make sure the laser level is properly calibrated before use. A poorly calibrated laser level can give you inaccurate readings, which can lead to costly mistakes.

There are many different types of laser levels available, each with its own set of features and benefits. Some are designed for indoor use, while others are designed for outdoor use. Some are self-leveling, while others require manual adjustment. Choose the type that best suits your needs and budget. And remember, safety first! Always wear appropriate eye protection when working with laser levels.

FAQs About Perpendicular Lines

7. Q

A: Parallel lines run alongside each other and never intersect. Think of railroad tracks. Perpendicular lines, on the other hand, intersect at a 90-degree angle.

8. Q

A: Nope! That’s geometrically impossible. A line can only be either perpendicular or parallel to another line, not both at the same time.

9. Q

A: Absolutely! Look at the corners of most buildings, the intersection of roads at a right angle, or even the way a picture frame hangs on the wall (when it’s straight, that is!). The keyword term, perpendicular, is applicable in these context.

10. Q

A: You might use them when hanging pictures, building shelves, or even parking your car straight. Understanding perpendicularity can help you make things look more aesthetically pleasing and function better.

← How To Tell If A Capacitor Is Polarized | Is Pcb Electrical Or Electronics →