Parallel Lines
1. The Straight Story on Parallel Lines
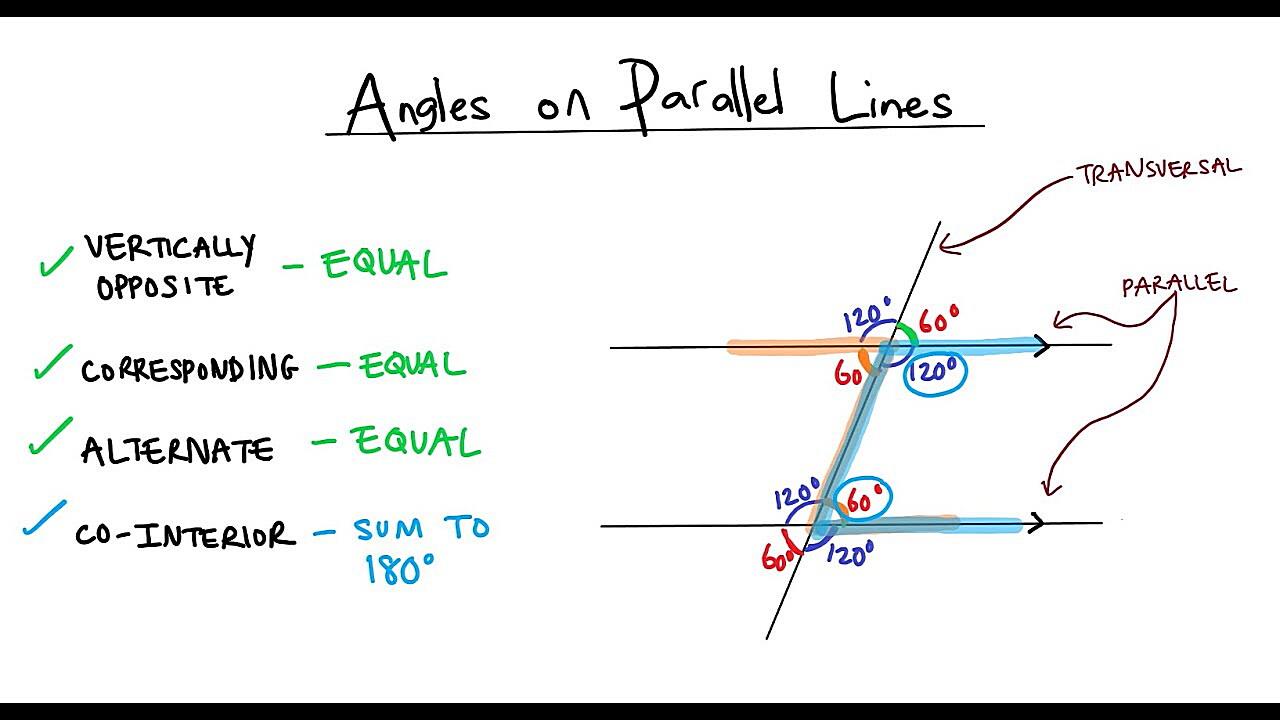
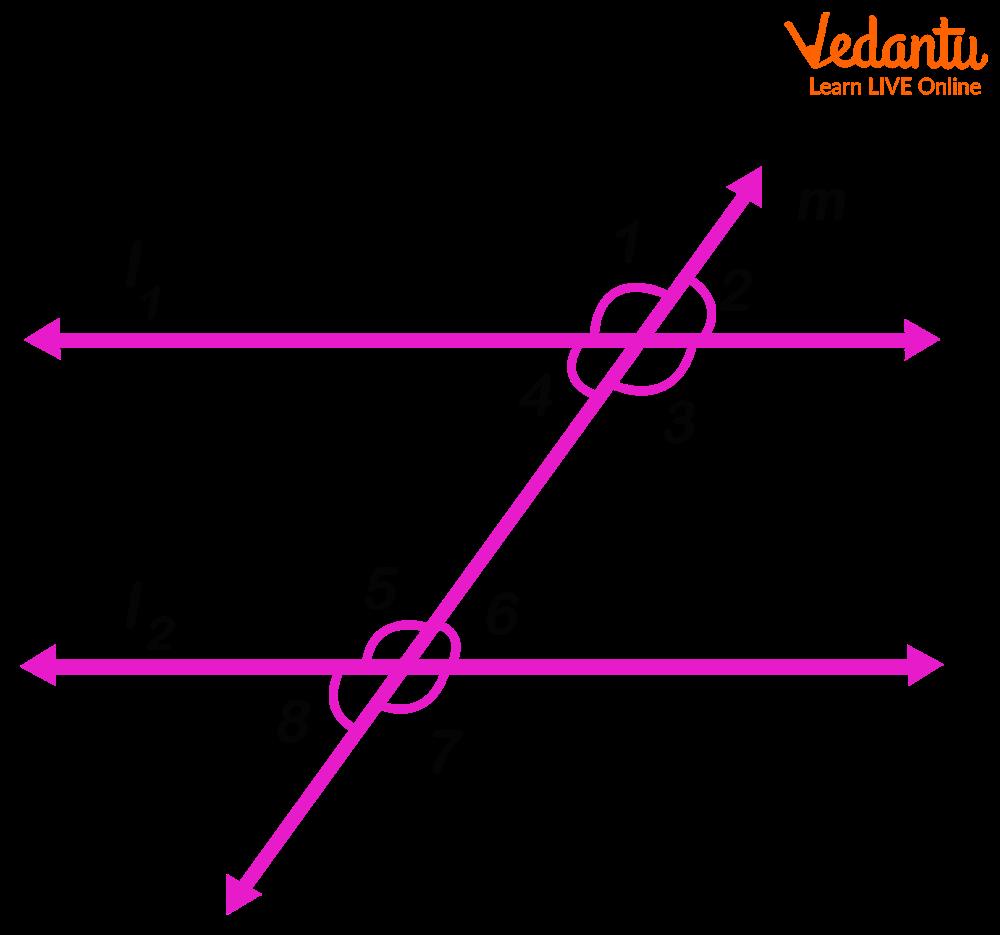
Okay, let’s talk about parallel lines. We’re all familiar with them, right? Two lines cruising along, never touching, never intersecting, always keeping their distance. Like introverts at a party — perfectly content to exist in the same space but avoiding eye contact at all costs. But what if I told you that under the right (or maybe the wrong) circumstances, these aloof lines could actually meet? Mind. Blown.
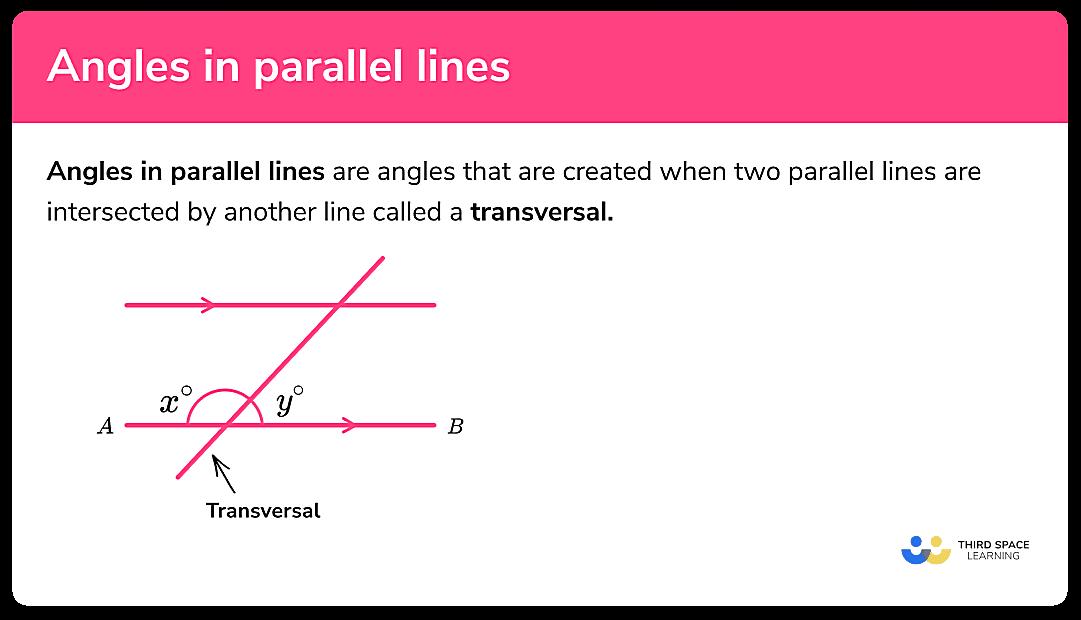
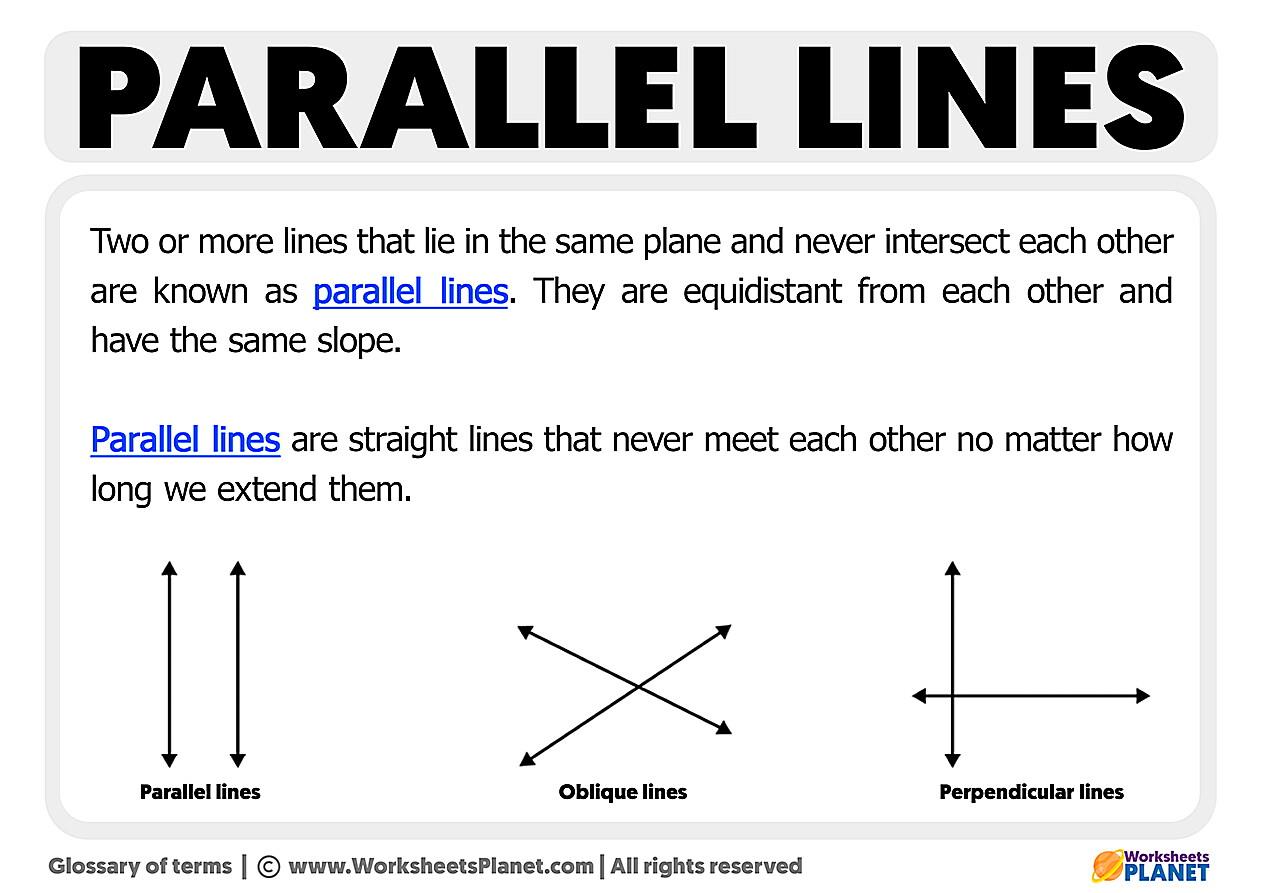
In the realm of Euclidean geometry, the geometry most of us learned in school, parallel lines are the epitome of non-interaction. They’re defined as lines in a plane that never intersect, no matter how far you extend them. Think of railroad tracks stretching into the horizon. They look like they might converge way off in the distance, but that’s just an optical illusion. In theory, they remain perfectly parallel, each steel rail eternally separated by the same precise gap.
But here’s the twist: our everyday understanding of space and geometry isn’t the only game in town. There are other kinds of geometry, ones that bend the rules a little (or a lot!). It’s like realizing that not everyone plays Monopoly by the official rules. Some people sneak money from the bank! (Don’t be that person.)
We’re talking about things like spherical geometry, where you’re dealing with shapes drawn on the surface of a sphere instead of a flat plane. This opens up a whole new world of possibilities, and the concept of “parallel” gets a serious makeover. Imagine drawing lines on a globe — things aren’t quite as straightforward as they seem on a piece of paper.
The Spherical Surprise
2. Curvature Changes Everything
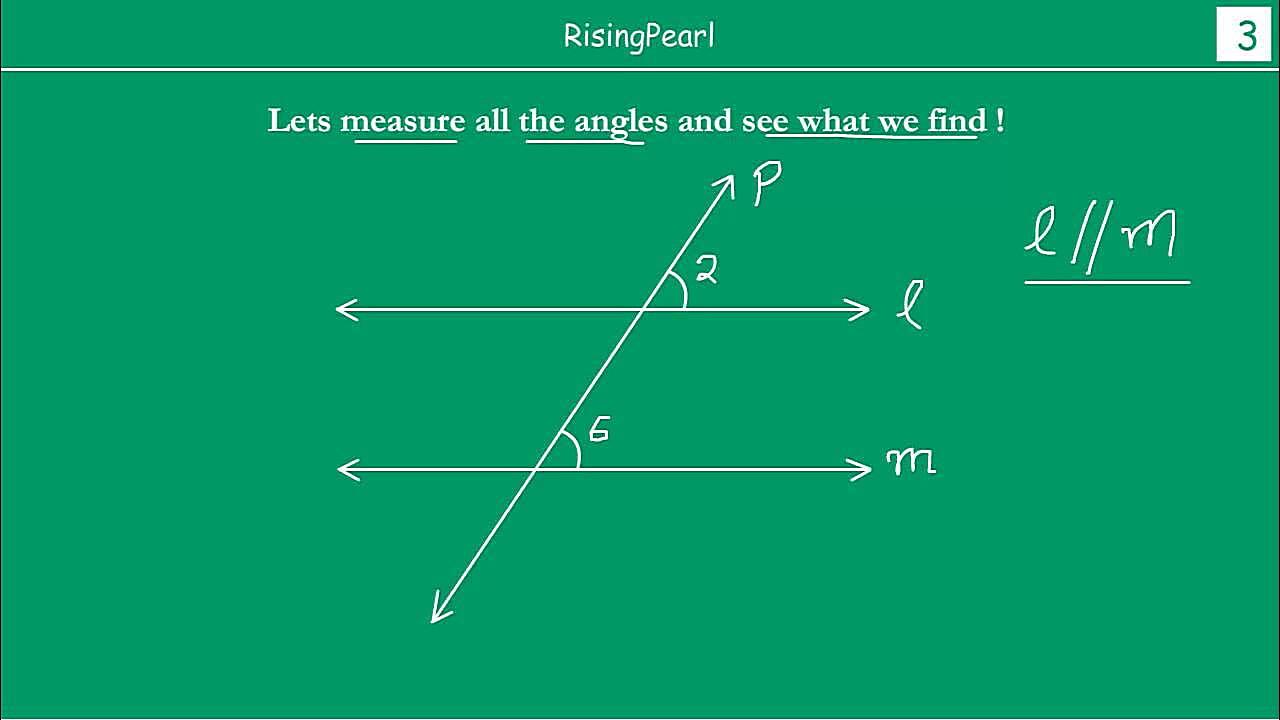
Now, let’s dive into spherical geometry. Think of the Earth. Lines of longitude (also known as meridians) are a great example. They’re all perpendicular to the equator, and they appear to be parallel at the equator, right? But here’s the kicker: they all converge at the North and South Poles. Those lines, which start out looking so independent and aloof, eventually end up sharing a rather intimate moment at the top and bottom of the world.
So, in spherical geometry, lines that are “parallel” at one point can definitely intersect at another. It’s like they’re playing a game of hide-and-seek, pretending to ignore each other for a while before dramatically reuniting. This happens because the surface is curved. The curvature forces the lines together, overcoming their initial aversion to intersection.
This isn’t just some abstract mathematical concept, either. It has real-world implications for things like navigation and mapping. Pilots and sailors need to understand spherical geometry to accurately chart their courses, because a straight line on a flat map isn’t necessarily the shortest distance between two points on the Earth. It’s a fascinating reminder that our intuition about the world can sometimes be misleading.
The key takeaway here is that the definition of “parallel” is dependent on the geometry you’re working with. Euclidean geometry says no intersection ever. Spherical geometry says “Hold my beer, I got this.” Its like the difference between saying all dogs are fluffy and then seeing a chihuahua. Geometry, just like life, has surprises.
Projective Geometry
3. Vanishing Points and Infinite Intersections
But wait, there’s more! Let’s introduce another contender: projective geometry. This is where things get really mind-bending. In projective geometry, parallel lines do intersect… at infinity! It’s like they’re having a secret rendezvous in a dimension we can’t quite grasp.
Think about standing on a long, straight road. As the road stretches into the distance, the two edges seem to get closer and closer until they eventually converge at a single point on the horizon. That point is the vanishing point, and in projective geometry, it represents the intersection of those “parallel” lines at infinity.
This concept is used extensively in art and computer graphics to create the illusion of depth and perspective. Artists use vanishing points to make objects appear smaller as they recede into the distance, creating a realistic sense of space. So, the next time you’re admiring a painting or playing a video game, remember that projective geometry is working its magic behind the scenes.
While the idea of lines meeting at infinity might seem a little abstract, it’s a powerful tool for understanding how we perceive the world. It reminds us that our perception is not always a perfect representation of reality, and that there are other ways of thinking about space and geometry that can be incredibly useful.
The Takeaway
4. Geometry isn’t One-Size-Fits-All
So, can parallel lines meet? The answer is a resounding “It depends!” In Euclidean geometry, the answer is a firm no. But in other geometries, like spherical or projective geometry, parallel lines can and do intersect, either at a point on a curved surface or at infinity.
The important thing to remember is that geometry isn’t just a set of rules and formulas; it’s a way of describing the properties of space. And space, as it turns out, can be a pretty weird and wonderful place. Different geometries are useful for different purposes, and each one offers a unique perspective on the nature of reality.
Thinking about these different geometries helps us understand that our everyday intuition about the world isn’t always the complete picture. There are hidden complexities and surprising possibilities that lie beneath the surface, waiting to be discovered. It’s a reminder to keep an open mind and to question our assumptions, because you never know when you might stumble upon a new and exciting way of looking at things.
Ultimately, the question of whether parallel lines can meet is a testament to the power of human imagination and our ability to create new and innovative ways of understanding the world around us. So, go forth and explore the vast and fascinating world of geometry — you might just be surprised at what you find.
FAQ
5. Frequently Asked Questions (Because Geometry Can Be Confusing!)
Got questions about parallel lines and their potential rendezvous? You’re not alone! Here are some common queries to clear up any lingering confusion:
Q: So, in the real world, do parallel lines actually meet?
A: Well, that depends on how you define “real world.” In the world of Euclidean geometry, which is a pretty good approximation of the world around us on a small scale, parallel lines don’t meet. But if you’re dealing with very large distances or strong gravitational fields (which can warp space), then the curvature of space becomes significant, and the rules of Euclidean geometry might not apply. In those situations, parallel lines could potentially converge.
Q: Is this all just theoretical mumbo-jumbo, or does it have practical applications?
A: It’s definitely not just theoretical mumbo-jumbo! As mentioned before, spherical geometry is crucial for navigation and mapping. And projective geometry is essential for art, computer graphics, and even architecture. These concepts might seem abstract, but they have tangible impacts on our daily lives.
Q: If parallel lines meet at infinity, does that mean infinity is a place?
A: Ooh, that’s a deep one! Infinity isn’t really a “place” in the traditional sense. It’s more of a concept — a way of representing something that goes on forever. When we say parallel lines meet at infinity in projective geometry, we’re simply saying that they converge at a point that is infinitely far away. It’s a mathematical convenience rather than a literal location.
Q: My brain hurts. Can I just go back to thinking parallel lines never meet?
A: Absolutely! If you’re not planning on becoming a topologist or a theoretical physicist anytime soon, there’s no shame in sticking with the Euclidean definition of parallel lines. But hopefully, this article has at least opened your mind to the possibility that there’s more to geometry than meets the eye!